サブグループの平均と範囲のコントロール XbarR チャートを効果的に使用するためのデータの合理的なグループ化
出典: Donald Wheeler 博士からご提供いただいた記事: [35] 合理的なグループ化。プロセス動作図の概念的な基礎 / 合理的なサブグループ化。プロセス動作チャートの概念的基礎、ドナルド J. ウィーラー。
翻訳者兼科学編集者: Sergey P. Grigoryev
記事への自由なアクセスは、記事に含まれる資料の価値を決して減じるものではありません。
管理図を効果的に使用する上で重要な点は、適切な質問に答える能力です。これを行うには、データをサブグループに分散する方法がデータの構造に対応している必要があります。これは通常、空間、時間、生産バッチなどの「小さな領域」からのデータを各サブグループにグループ化し、サブグループ内のデータが可能な限り均一になるようにすることを意味します。サブグループ内の変動を最小限に抑えることが強調されるのは、管理限界の計算に使用されるのはこの変動であるという事実から来ています。管理限界は平均範囲に依存し、平均範囲はサブグループ内のばらつきを反映する個々のグループの範囲に依存します。管理限界を設定するために使用されるのはサブグループ内の変動であり、サブグループ間の変動がどの程度許容されるかを決定します。
平均管理図によって提起される疑問は、「グループ内の変動に基づいて、グループの平均が必要以上に変動するか?」ということです。言い換えれば、「サブグループ内のばらつきを考慮すると、グループ平均間の差異は検出可能ですか?」
サブグループ範囲グラフでは、「サブグループ内の変動はサブグループ間で一貫していますか?」と尋ねられます。または、別の言い方をすると、「サブグループ内の平均変動を仮定すると、サブグループ間の変動の差は検出可能ですか?」
これら 2 つの質問の違いを、いくつかの例で説明します。
シートの厚さ
パッド入りパネル被覆材の製造に使用される幅 30 インチ (762 mm) のビニール シートは、自動プロセス コントローラーの制御下で押出成形されました。この自動プロセス コントローラーの入力デバイスは、ビニールの厚さを測定する従来のベータ スキャナーでした。エンジニアは、ビニール シートの左端から 10 インチの位置にある 1 つのトラックに沿った厚さの測定値を調査したいと考えたので、そのトラックのすべてのデータを収集し、サイズ 4 のサブグループを使用して XbarR サブグループ平均および範囲参照マップ上にプロットしました。 。
サイズ 4 のサブグループを使用することで、各サブグループが約 2 分のプロセス作業に相当することを保証しました。彼の意見では、これにより、各サブグループの押し出しプロセスに通常の変動 (共通の原因によるランダムな変動) が現れることが可能になりました。図 1 の平均管理図は、自動コントローラーが約 20 分のサイクルでプロセスを上下に調整していることを示しています。平均の厚さは 48.5 mm でしたが、5 ~ 6 分後には 49.5 mm になり、6 分後には 47 mm に低下する可能性があります。この厚さの変化は、真空形成時のビニールの加熱と伸縮に影響を与えました。この厚さの変化により、次のステップで無駄が生じましたが、平均して、ビニールは適切な厚さでした。
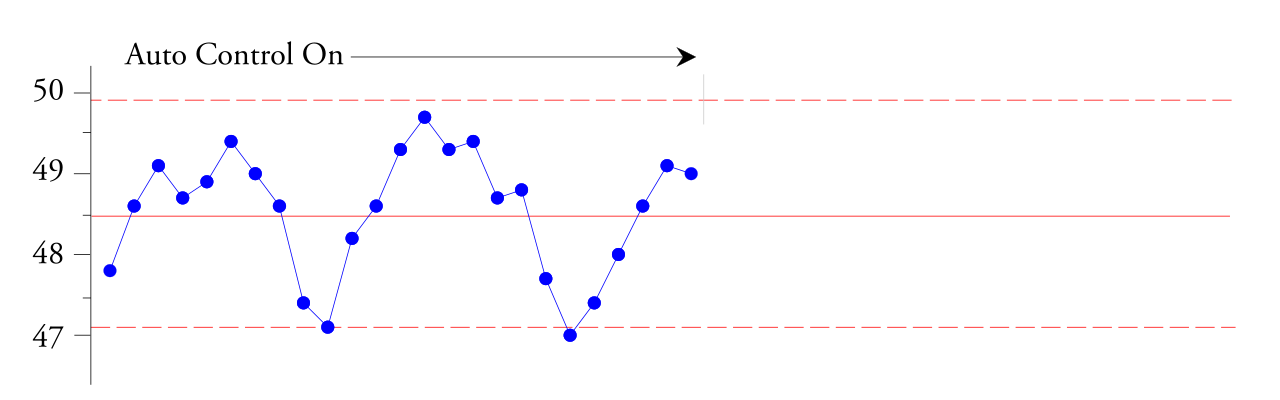
米。 1.自動制御時のビニールシートの平均厚さサブグループのXbarR管理図。
管理限界内の点は上下する傾向にあり、この自動プロセス コントローラーでは不十分であることがわかります。 減衰された 、良好な定常状態の応答を維持できず、支援が必要です。この XbarR コントロール カードを作成したエンジニアによると、私たちが見ている「正弦波を認識する」のは簡単です。図 1 で観察された現象に基づいて、エンジニアは自動プロセス コントローラーの電源を切りました。次の 45 分間に、図 2 の右側に示す新しい値が受信されました。
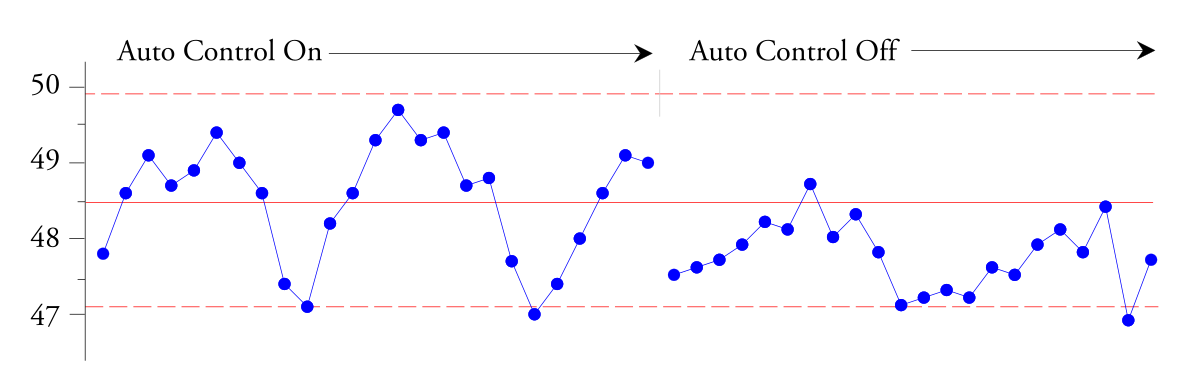
米。 2. ビニールシートの平均厚さサブグループのコントロール XbarR チャート (続き)。
これにより、シート厚さの変動の約半分が自動プロセスコントローラーによるものであることが確認されました。これらの変動により出力に欠陥が生じるため、この自動プロセス コントローラーはこれら 20 分のサイクルを排除するように適切に構成する必要があります。グラフの解釈から必要なアクションの定式化までのパスが、データのコンテキストとデータがどのようにサブグループに編成されるかによって左右されることに注目してください。
最大トルクまでの時間
ゴム配合物のバッチの硬化特性を特徴付けるには、各バッチのサンプルを実験室でテストする必要があります。このテストでは、ゴムサンプルが硬化する際のトルクを測定します。テスト結果は、最大トルクを達成するために必要な硬化時間でした。 3 人のオペレーターはそれぞれ、シフトごとに 5 回のゴムを生産したため、研究所は各オペレーターの 5 つの毎日の値をサブグループとして使用することにしました。これにより、シフトごとに 1 つのサブグループが作成され、サブグループ内の変動は各オペレーターのバッチ間の変動、サブグループ間の変動はオペレーターごとおよび日ごとの変動となります。すべてのオペレーターが同じゴム工場を使用して同じ製品を生産したため、サブグループの平均と範囲の XbarR チャートを作成するときに予測可能なプロセスが表示されることが期待されました。
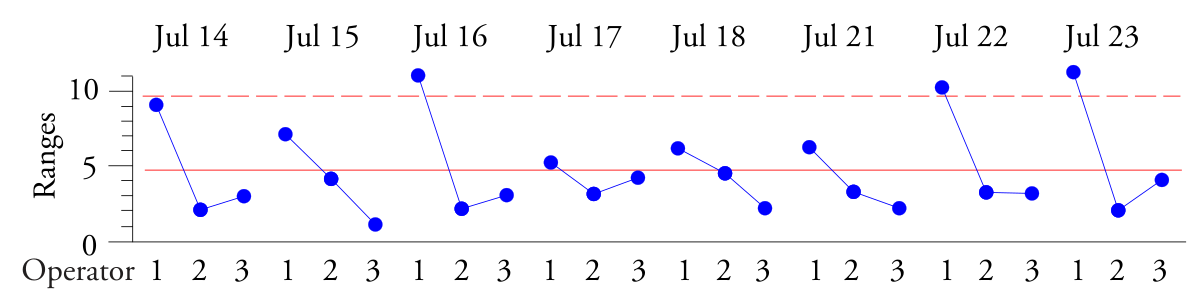
米。 3. 最大トルクまでの時間のサブグループ範囲の R マップを制御します。
グループ範囲の R マップは、高値、低値、低値の繰り返しパターンを示します。オペレーター 1 によって生成されたバッチは、オペレーター 2 および 3 によって生成されたバッチよりも多くのばらつきを示します。オペレーター 1 は 30 年の経験を持つ上級オペレーターでしたが、バッチを適切に混合しませんでした。これは、オペレーター 1 が視力を失い、手動で混合できるほどよく見えなくなったためであることが判明しました。
繰り返しになりますが、データを解釈する鍵となるのは、管理図上でデータを整理することです。グループ範囲の XbarR 管理図は、サブグループ内の一貫性の欠如を示しており、各サブグループを 1 つのステートメントで識別することで、図 3 に示すパターンを理解できるようになります。サブグループの平均と範囲の XbarR 管理図。サブグループ間で発生する位置の変化は、サブグループ平均の X マップ上に表示されます。異なるサブグループ内で発生する変動の変化は、グループ範囲の R マップに表示されます。いずれの場合も、生じる差異を検出するための基準を決定するのは、サブグループ内の変動です。これを理解することが、観測データを効果的に分析する鍵となります。
上記の最初の例では、自動プロセス コントローラーを無効にする簡単な実験を提供する順序回路でした。 2 番目の例では、データ構造と一致したアプローチにより、視覚障害のあるオペレーターの発見につながりました。どちらの場合も、図を文脈に沿って解釈することで発見が得られました。データの収集と構築の方法と一致するこのように考える意欲は、プログラムすることはできません。それは誰かが時間と労力をかけてチャートを見て考えることにかかっています。これは、これまでも、そしてこれからも、プロセス動作管理図を効果的に使用する上で不可欠な部分です。
一部のデータセットでは、合理的なサブグループ化が非常に簡単になります。ただし、一部のデータ セットでは、データをサブグループに分割する方法が複数ある場合があります。次の例はこのカテゴリに分類されます。
射出成形ジョイントヘッド
スイベルジョイントは射出成形により一度に4個ずつ製造されます。このデータの収集時点では、この製造方法は材料と技術の両方の変化を表していました。そのため、量産に入る前に工程認証を受ける必要がありました。マネージャーの Dave は、認証前にプロセス動作チェックリストを使用してプロセスを評価することにしました。
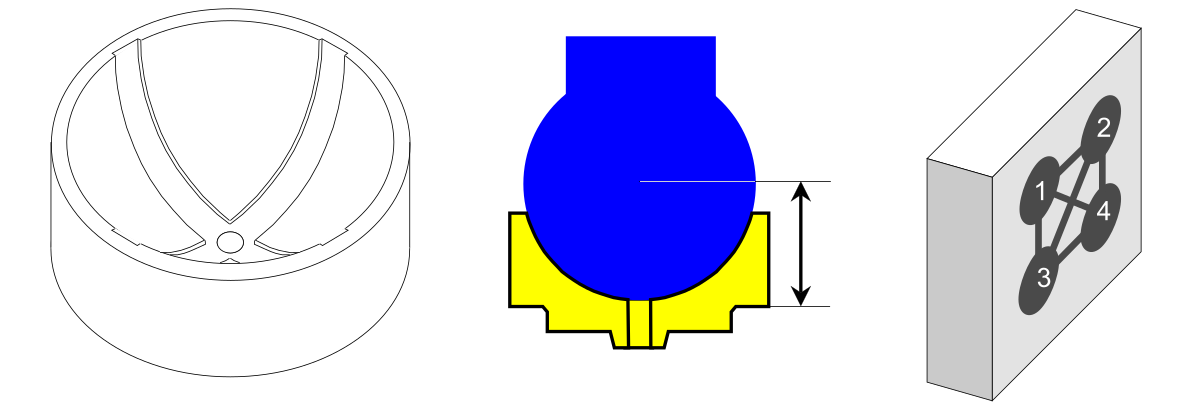
米。 4. ボールカップリング、厚さサイズ、および 4 つのキャビティを備えた金型。
金型は 1 つしかなかったため、認証プロセスに関与したのは 1 台のプレス機と 1 人のオペレーターだけでした。データは、100 分の 1 ミリメートル単位で測定されたボール カップリングの有効厚さでした。ボール カップリングの片側は凹状だったため、この厚さを測定するために特別なゲージを設計して製造する必要がありました。ゲージ測定では、厚さが 12.00 ミリメートルを超えていることがわかりました。デイブは 1 日に 4 回、プレス機に行き、連続した 5 回のプレス サイクルで製造された部品を集めました。各サイクルでは 4 つの部品 (各キャビティから 1 つ) が製造されたため、2 時間ごとに 20 個の部品を測定する必要がありました。デイブは慎重に、サイクルと各部品がどのキャビティから来たのかを記録していました。
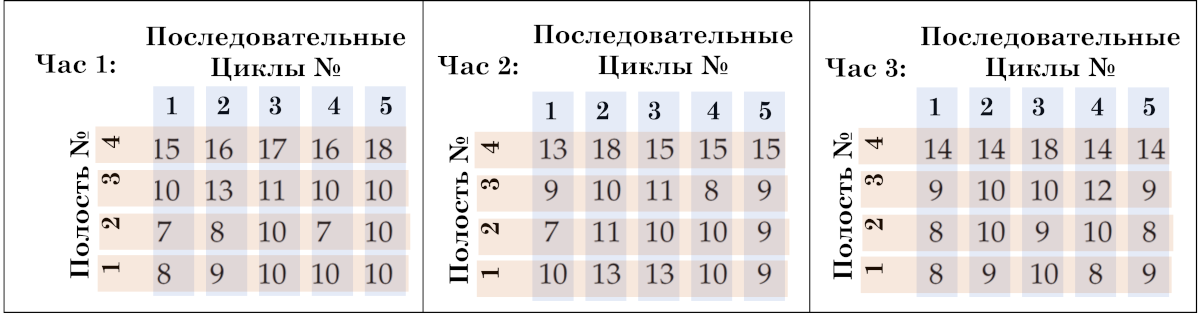
米。 5.時間ごとのボールカップリング厚さデータの構造。時間、連続セルクル、キャビティ。
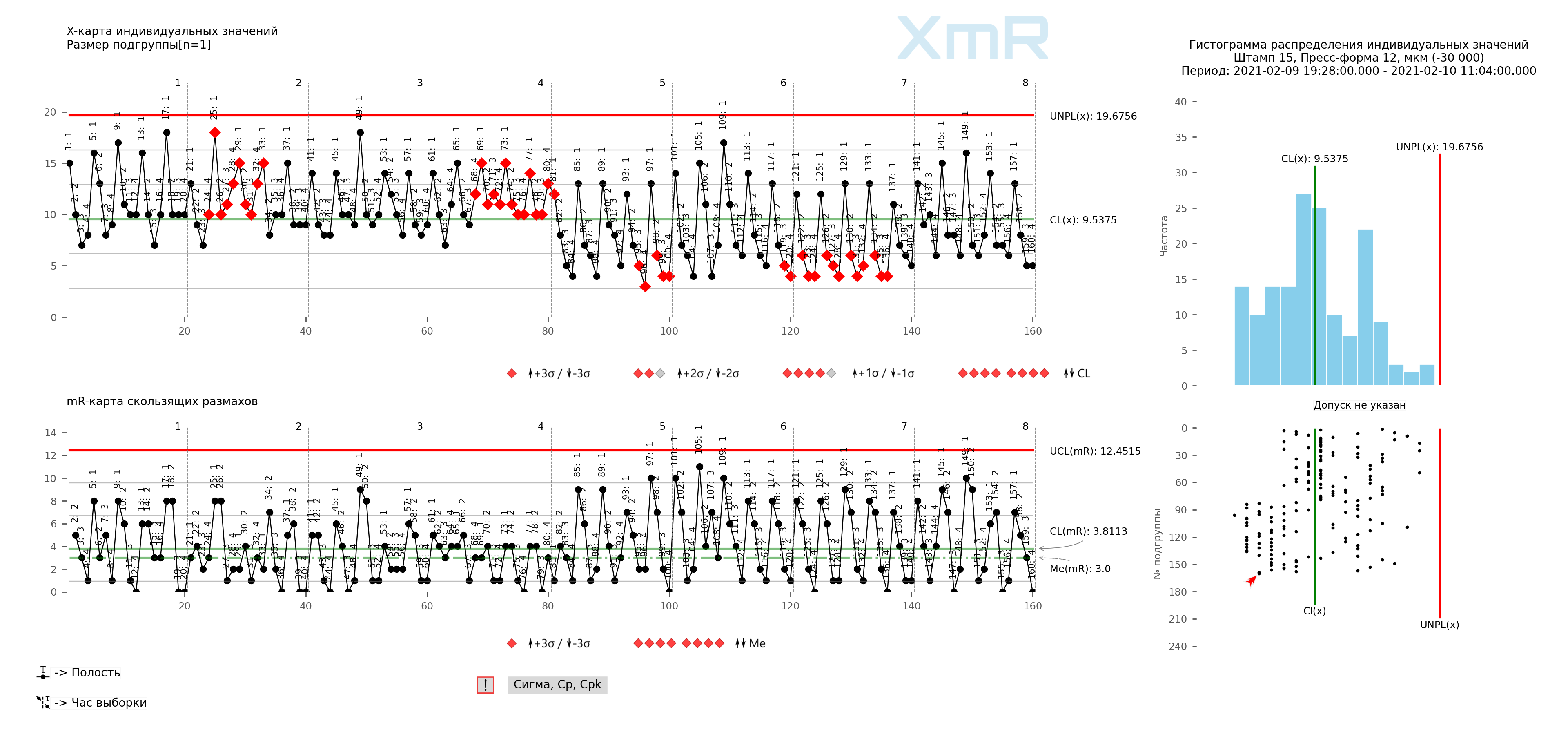
米。 6. ボールカップリングの厚さに関する時間ごとのデータのプロセス進捗チャート(個別の値とスライド範囲のXmRチャート)の構造。垂直の仕切り: 時間、すべてのポイントのサイン: 金型キャビティ。 図面は当社が開発したものを使用して作成されました 「シューハート管理図 PRO-Analyst +AI(Windows、Mac、Linux用)」 。
これらのデータには、特定可能な変動源が 3 つあります。時間ごとの変動があり、図 5 では 20 個の値の異なるセット (ブロック) で表されています。サイクルごとの変動があり、図 5 のさまざまな列 (1、2、3、4、 5)。また、キャビティごとにばらつきがあり、図 5 では異なる線 (1、2、3、4) で表されています。
サブグループの平均と範囲の XbarR 管理図でそれらをグループ化するさまざまな方法と、サブグループへのデータの各編成が管理図の解釈に及ぼす影響を見ていきます。認定プロセスのために、デイブは 6 日間のデータを収集しました。簡潔にするために、最初の 2 日間のデータのみを使用します。
完全なデータセットとサブグループへの最初の編成を図 7 に示します。4 つの値の各列を使用してサブグループを定義するため、160 個の値がサイズ n=4 の 40 のサブグループに編成されます。異なる時間 (1、2、3 など) のデータは、異なるサブグループに属します。時間を変更すると、サブグループも変更されます。したがって、この最初のデータのサブグループへの編成では、サブグループ間に時間ごとの差異 (日ごとの差異も同様) が現れると言えます。ここで、XbaR 平均チャートは次の質問をします。
質問 #1: 時間ごとまたは日ごとに顕著な違いはありますか?
図 8 では、異なるサイクル (1、2、2、4、5) からのデータが異なるサブグループに含まれています。サイクルを変更すると、サブグループも変更されます。したがって、これらのデータのこの最初の編成では、サブグループ間でサイクル間の差異が現れると言えます。ここで、平均サブグループ グラフは次の質問もします。
質問 #2: サイクル間に目立った違いはありますか?
図 8 では、異なるキャビティ (1、2、3、4) からのデータが同じサブグループ内にあります。キャビティを変更する場合、サブグループを変更する必要はありません。したがって、これらのデータのこの最初の編成では、サブグループ内で虫歯間の差異が現れると言えます。したがって、ここでグループ範囲グラフは次の質問をします。
質問 3: 空洞間の違いは一貫していますか?

米。 7. データをサブグループに編成する最初の方法。
平均値 - 9.54;平均範囲は 7.63 で、図 8 に示す管理限界が得られます。グラフの線を区切ることで、各時間を個別に参照できるようになり、読みやすくなります。制限を超える点はありませんが、サブグループ平均プロットには明確なシグナルがあります。 20 個中 20 個の平均が中心線より上にあり、次に 20 個中 19 個が中心線より下にある場合、1 日目と 2 日目には大きな違いがあります。サブグループ範囲グラフでは、日ごとの差異も表示できます。したがって、質問 1 (時間または日の間に顕著な違いはありますか?) には明確な「はい」で答え、質問 2 (サイクル間に顕著な違いはありますか?) には否定で答え、質問 3 (違いは一貫していますか) に答えます。 ? 空洞の間?) おそらく「いいえ」です。
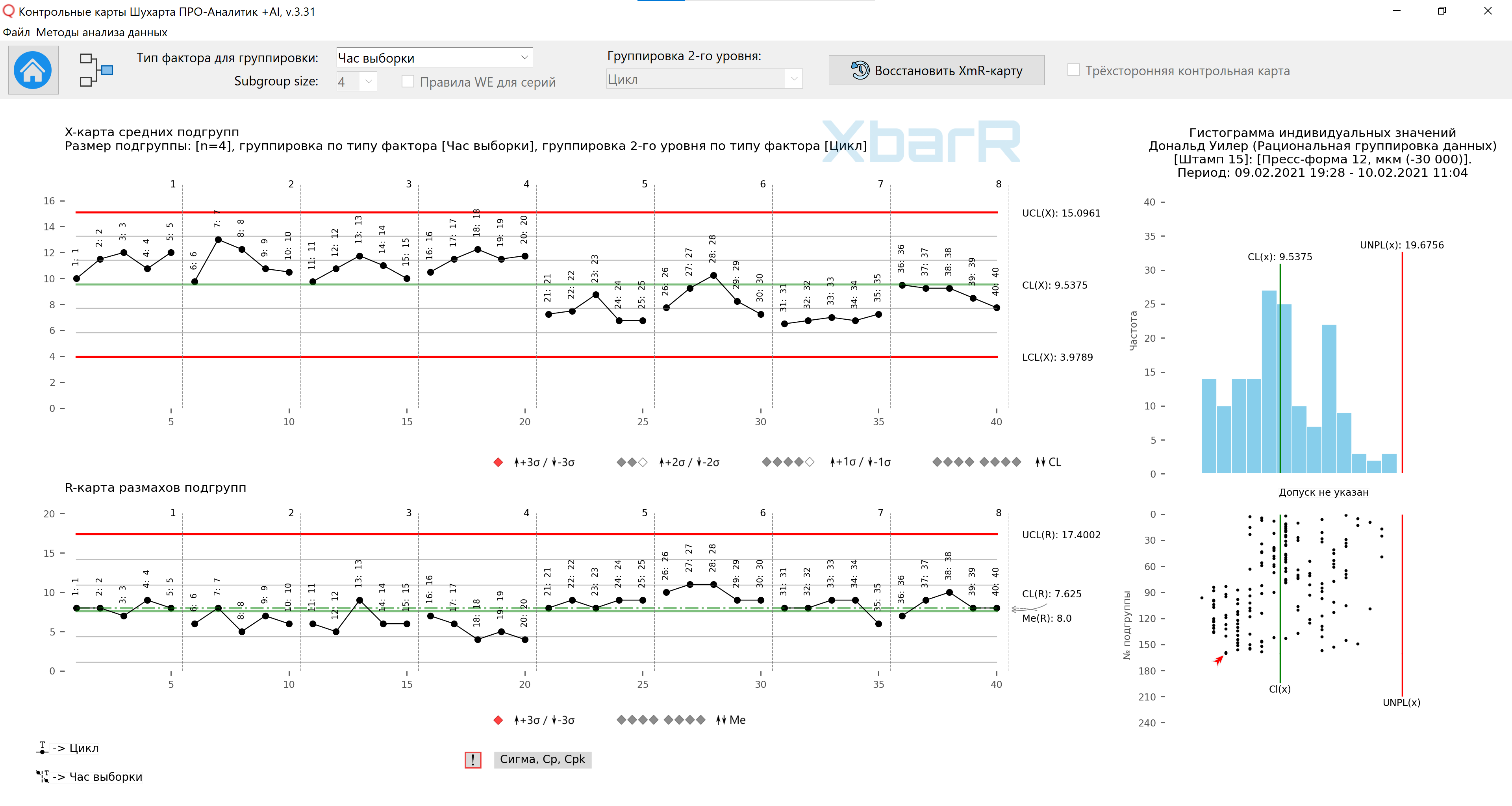
米。 8. サブグループ内のデータを編成する最初の方法のサブグループの平均と範囲のマップ。 1 ~ 8 の値で系列を分割する垂直線 - サンプリング時間、すべての点の署名 - サイクル番号。 図面は、当社が開発したものを使用して作成されました。 「シューハート管理図 PRO-Analyst +AI(Windows、Mac、Linux用)」 ユニークなものを使って 合理的なデータグループ化のための自動化機能 選択した種類の変動要因 (因子を含む列) およびサブグループのサイズごとに、サブグループの平均と範囲の XbarR グラフを構築します。
データをサブグループに編成する 2 番目の方法
このデータを整理する 2 番目の方法を図 9 に示します。そこでは、5 つの値の各行を使用してサブグループを定義するため、最終的にサイズ n=5 の 32 個のサブグループが得られます。ここで、異なるクロック (1:、2:、3: など) からのデータは、異なるサブグループに属します。時間を変更すると、サブグループも変更されます。したがって、2 番目の組織では、サブグループ間で 1 時間ごと (および 1 日ごと) の差異が現れると言えます。ここで、平均サブグループ グラフは次の質問をします。
質問 #4: 時間ごとまたは日ごとに顕著な違いはありますか?
図 9 では、異なるサイクル (1、2、3、4、5) からのデータが同じサブグループ内にあります。サイクルを変更する場合、サブグループを変更する必要はありません。したがって、これらのデータの 2 番目の構成では、サブグループ内でサイクル間の差異が現れると言えます。ここで、グループ範囲図は次の質問をします。
質問 #5: サイクル間の違いは一貫していますか?
図 9 では、これらの異なるキャビティ (1、2、3、4) が異なるサブグループに属しています。キャビティを変更すると、サブグループが変更されます。したがって、これらのデータの第 2 の整理では、サブグループ間で虫歯間の差異が現れると言えます。ここで、サブグループ平均プロットは次の質問も問いかけます。
質問 #6: キャビティ間に顕著な違いはありますか?
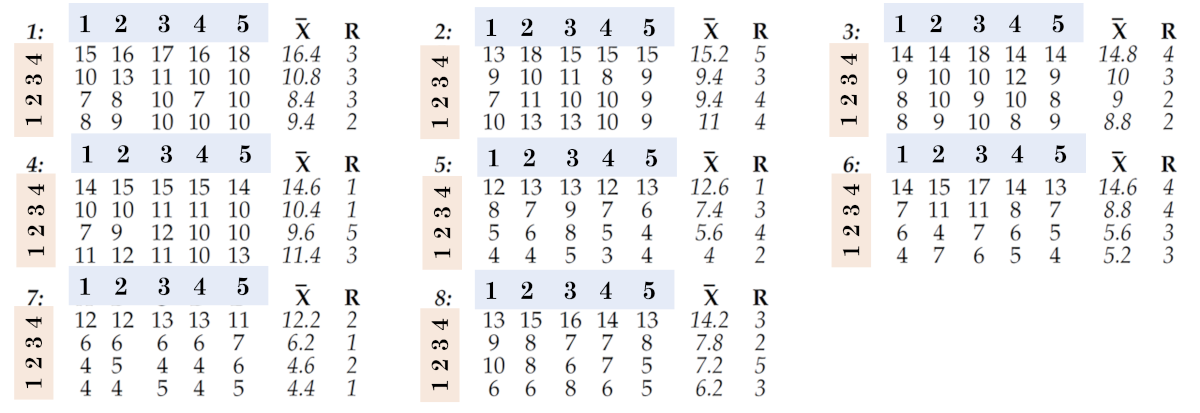
米。 9. データをサブグループに編成する 2 番目の方法。
平均値 - 9.54;平均範囲は 2.84 で、図 10 に示す管理限界が得られます。32 個の平均値のうち 20 個が管理限界外にあるため、解釈すべき信号がたくさんあります。 2 日間の間には顕著な違いがあり、4 つの虫歯の間には顕著な違いがあります。さらに、サイクル間の変化はサブグループ間で一貫しているように見えます (サブグループ範囲の R マップ)。
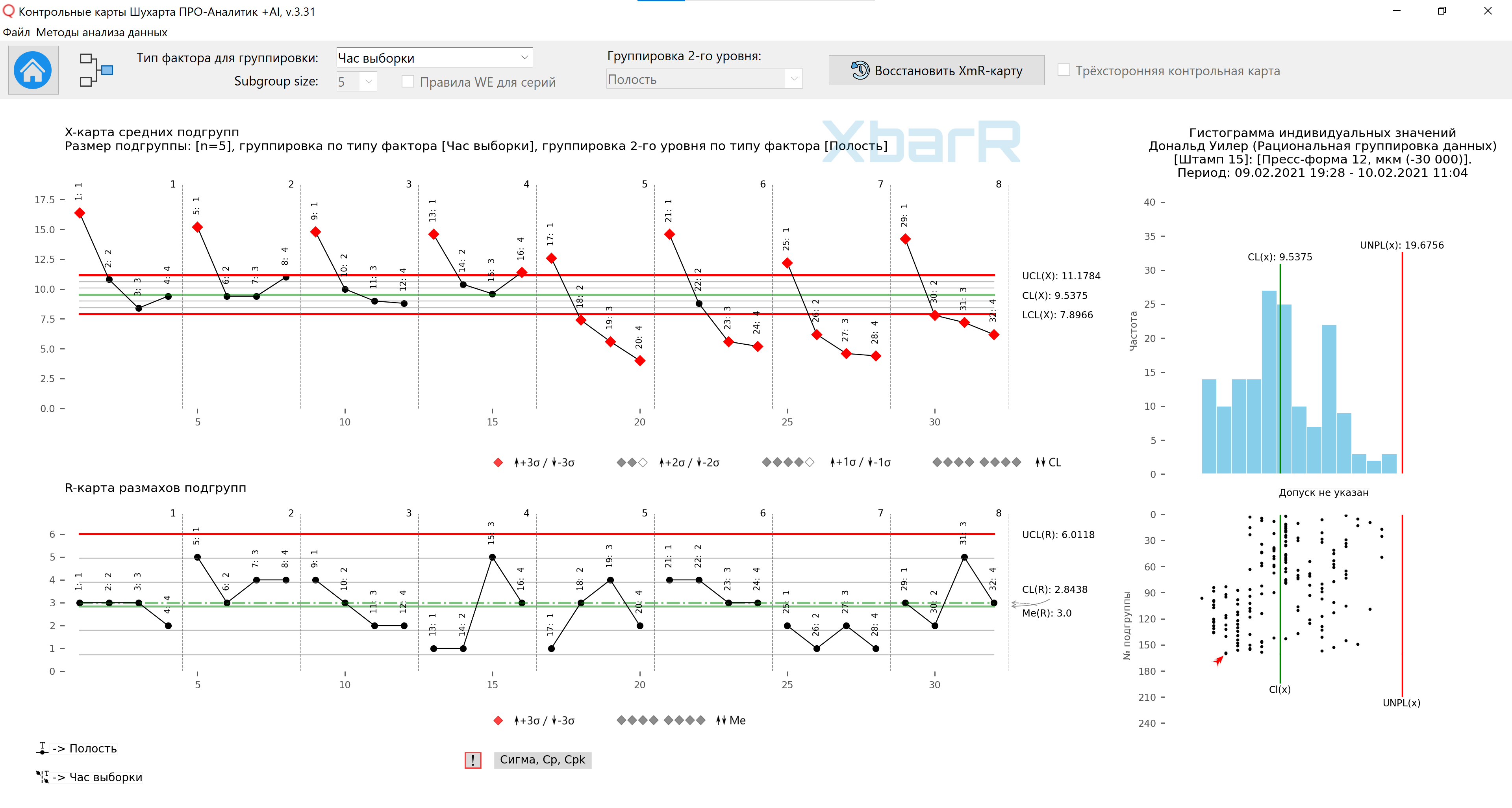
米。 10. サブグループ内のデータを編成する 2 番目の方法のサブグループの平均と範囲の図。 1 ~ 8 の値で系列を区切る縦線はサンプリング時間です。すべてのポイントの署名 - キャビティ番号。図面は当社が開発したものを使用して作成されました。 「シューハート管理図 PRO-Analyst +AI(Windows、Mac、Linux用)」 ユニークなものを使って 合理的なデータグループ化のための自動化機能 選択した種類の変動要因 (因子を含む列) およびサブグループのサイズごとに、サブグループの平均と範囲の XbarR グラフを構築します。
上記の 2 つの方法でデータをサブグループに整理することは技術的には正しいのですが、データに対して同じ質問をしていないため、実際には同じではありません。この違いを理解するには、質問 3 と質問 6 を検討してください。
データを最初に整理した結果、質問 #3:「空洞間の違いは一貫していますか?」という結果になりました。図 8 のグループ範囲図は、この質問に肯定的に答えています。キャビティ間の差は一定です。
2 番目の組織化により、「キャビティ間に顕著な違いはありますか?」という質問 #6 が生じました。図 10 の平均的なサブグループのグラフは、この質問に肯定的に答えています。 4 つのキャビティ間には顕著な違いがあります。キャビティ (1) では、他のキャビティよりも厚い部品が生成されます。
質問 3 と質問 6 の違いを理解し、その違いを利用して質問に答える方法を理解するまでは、合理的なサブグループ化を理解することはできません。これは練習と思考が必要なスキルです。次のセクションの質問に答えて練習できます。
データをサブグループに編成する 3 番目の方法
Dave は、以前のデータのサブグループへの編成を一切使用しませんでした。代わりに、図 11 に示すように、データをサブグループに編成する方法を認定テストに使用しました。再び 5 つの値の各行をサイズ 5 のサブグループとして使用するため、サブグループは 2 番目の組織と同じですが、今度は異なる方法で編成します。 32 のサブグループを含む 1 つのチャートの代わりに、キャビティごとに個別のチャートが作成されます。
図 10 では、キャビティとサイクルを固定しながら、サブグループを時間ごとに変更しますか?
それでは、サブグループ内またはサブグループ間で時間ごとの違いを見つけることができるでしょうか?
それでは、時間ごとの差異は範囲グラフまたはサブグループ平均マップのどこに表示されるのでしょうか?
図 10 では、固定クロックとキャビティを使用して、サイクルからサイクルに移動するときにサブグループを変更しますか?
それでは、サブグループ内またはサブグループ間のサイクル間の違いを見つけることができるでしょうか?
それでは、サイクル間の差はどこに現れるのでしょうか:範囲チャート上、それとも平均マップ上でしょうか?
図 10 では、クロックとサイクルが固定されているため、キャビティからキャビティに移動するときにサブグループを変更しますか?
では、虫歯の違いはどこにあるのでしょうか?
では、キャビティ間の違いはどこに現れるのでしょうか?
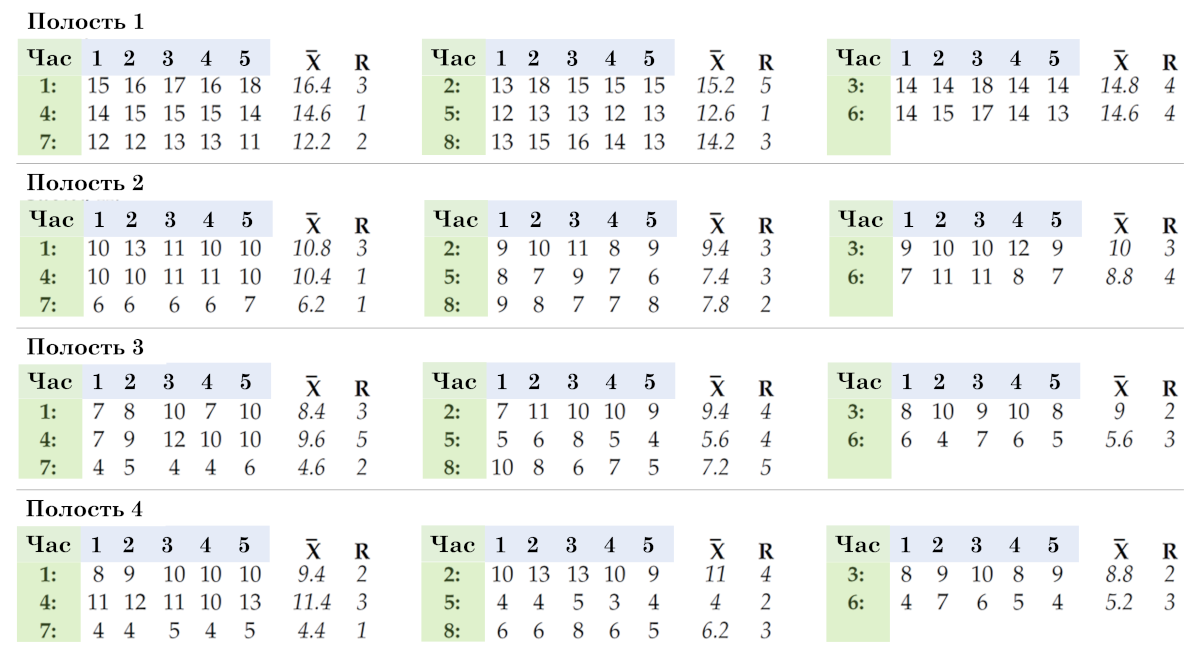
米。 11. データをサブグループに編成する 3 番目の方法。
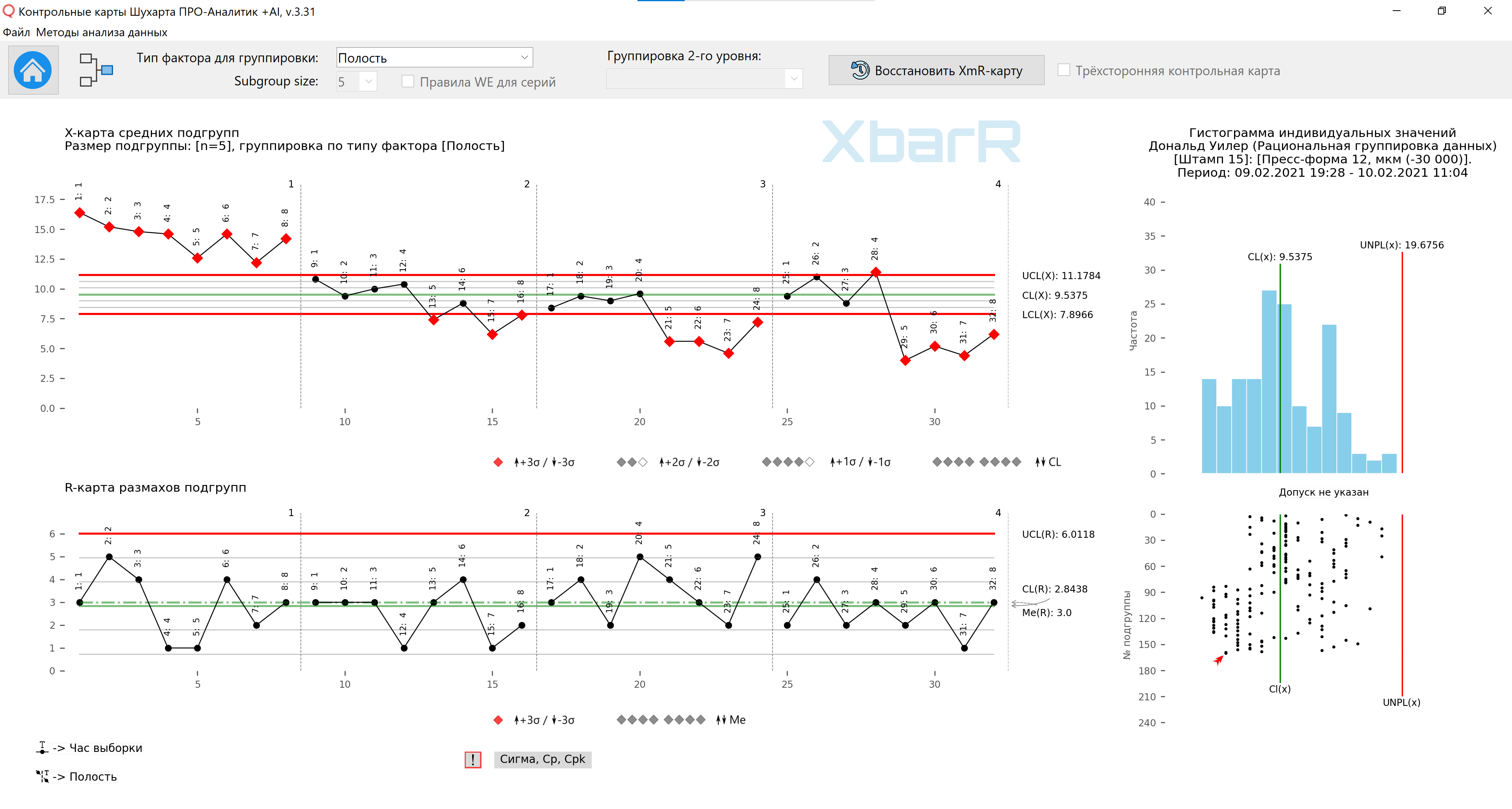
ライス。12. サブグループでデータを整理する3番目の方法のサブグループの平均と範囲のマップ。1から4までの値でシリーズを分割する垂直線-空洞の数。すべてのポイントの署名-サンプリング時間。この図は、当社が開発した 「シューハート管理図 PRO-Analyst +AI(Windows、Mac、Linux用)」 ユニークなものを使って 合理的なデータグループ化のための自動化機能 選択した種類の変動要因 (因子を含む列) およびサブグループのサイズごとに、サブグループの平均と範囲の XbarR グラフを構築します。
4 つの図をすべて同じ縦軸スケールにプロットすることで、キャビティ間の違いを示します。明らかに、キャビティ (1) により部品が厚くなり、キャビティ (2) はキャビティ (3) および (4) よりわずかに厚くなります。これらのグラフに基づいて、デイブはフォームを調整する必要があることを認識しました。キャビティ (3) と (4) は公差範囲内でかなり適切に中央に配置されていたため、彼は工具店にキャビティ (1) と (2) の後ろにシムを配置するように依頼しました。
スパン図で変動の原因は何ですか?時計?サイクル?虫歯?
平均チャートに変動の原因は何ですか?時計?サイクル?虫歯?
では、上記の平均チャートの管理限界外の点は何を意味するのでしょうか?
前の質問で問題が発生した場合は、この記事をもう一度読む必要があるかもしれません。
図 12 の管理図データの処理を続行し、実行ごとの管理限界機能を使用して、目に見える特徴に基づいてデータ実行を個々のキャビティ領域に分割し、金型の前後のさまざまなプロセスの機能の確認を取得できます。クリーニング。
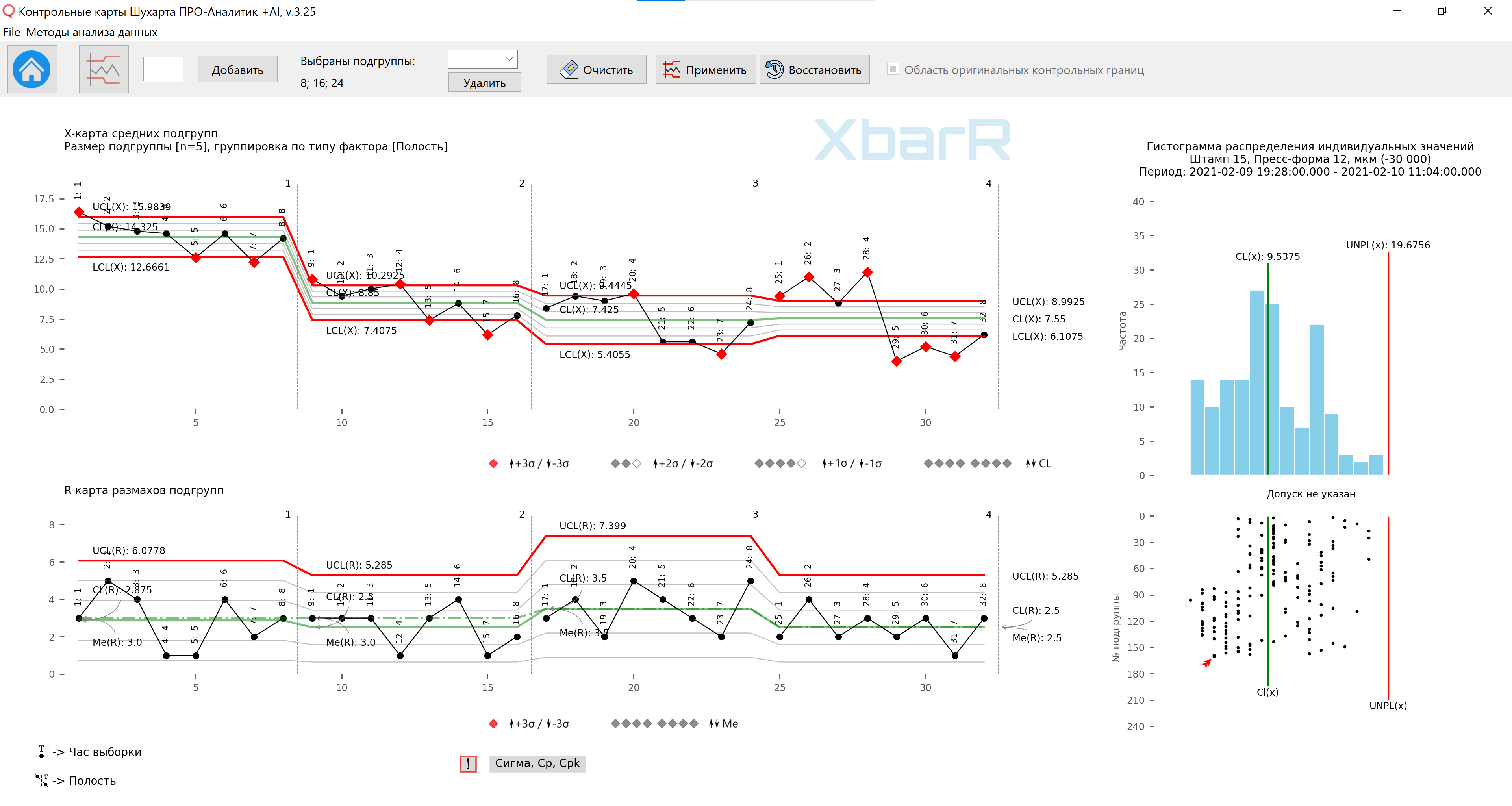
米。 13. 個々の一連の点の管理限界を使用してデータをサブグループに編成する 3 番目の方法のサブグループ平均と範囲のマップ。 1 ~ 4 の値で系列を分割する垂直線 - キャビティの数。すべてのポイントの署名 - サンプリング時間。図面は当社が開発したものを使用して作成されました 「シューハート管理図 PRO-Analyst +AI(Windows、Mac、Linux用)」 ユニークなものを使って 合理的なデータグループ化のための自動化機能 関数を使用して、選択した種類の変動ソース (因子を含む列) とサブグループのサイズによるサブグループの平均と範囲の XbarR グラフを構築します。 個々のサブグループ系列の管理限界を構築する 。
米。 14. 個々の一連の点の管理限界を使用してデータをサブグループに編成する 3 番目の方法のサブグループ平均と範囲のマップ。 1 ~ 4 の値で系列を分割する垂直線 - キャビティの数。すべてのポイントの署名 - サンプリング時間。図面は当社が開発したものを使用して作成されました 「シューハート管理図 PRO-Analyst +AI(Windows、Mac、Linux用)」 ユニークなものを使って 合理的なデータグループ化のための自動化機能 関数を使用して、選択した種類の変動ソース (因子を含む列) とサブグループのサイズによるサブグループの平均と範囲の XbarR グラフを構築します。 個々のサブグループ系列の管理限界を構築する 。
まとめ。データをサブグループに整理する
このデータをサブグループに編成する 3 つの方法はすべて技術的には正しいですが、実質的には同等ではありません。組織が異なれば、データについて異なる質問をし、データについて異なる仮定を立てます。
図 7 と図 8 でデータをサブグループに編成する最初の方法では、キャビティ間の一貫性をテストし、クロックとサイクル間の違いを探します。
図 9 と図 10 でデータをサブグループに編成する 2 番目の方法では、実行ごとの一貫性をテストし、クロック間およびキャビティ間の差異を探します。なぜこの組織は最初の組織よりも敏感なのでしょうか?
図 11 および 12 でデータをサブグループに編成する 3 番目の方法でも、サイクル間の一貫性をテストし、時間間およびキャビティ間の差異を探しますが、キャビティを別のチャートに配置することで (図 12)、識別が容易になります。時間ごとと日ごとのプロセスの違い。このデータを整理する 3 つの方法のうち、3 番目が最適です。
賢いデータのグループ化
サブグループの平均と範囲のチャートで質問の答えを得るための鍵は、XbarR チャートの 2 つの部分がどのように異なる質問をするのかを理解することです。サブグループ内に配置する変動源とサブグループ間に配置する変動源によって問題を制御します。互いに異なる可能性があるものは、異なるサブグループに配置する必要があります。同じである可能性があるものは、同じサブグループに配置する必要があります。
たとえば、2 つの測定値を同じサブグループ (n=2) にまとめた場合、2 つの値は本質的に同じ条件下で取得されたと結論付けられます。この判断要素こそが、あなたのサブグループを合理的なものにするのです。そのような判断がなければ、あなたのサブグループはおそらく非合理的になるでしょう。
異なるものを意図的にグループ化してはいけません。 各サブグループは論理的に同種である必要があります。リンゴ、オレンジ、バナナを一緒にすると、良いフルーツサラダができるかもしれませんが、結果的には悪いサブセットができてしまいます。幸いなことに、スコープ チャートは、さまざまなものを体系的にサブグループにグループ化するときに警告を発します。図 15 は、図 8 の範囲チャートを示しています。ここでは、各サブグループに 4 つのキャビティがすべてありました。

米。 15. データをサブグループに編成する最初の方法のサブグループ範囲のマップ。
図 15 で強調表示されているバンドは 1 シグマ バンドです。範囲値の 60 ~ 75% がこの範囲内に収まると予想されます。ここでは 40 のうち 36 が得られます。これは、90 パーセントが中心線から 1 シグマ以内にあります。グループ スパンが中心線にまたがる場合、グループ化された異なるもののサブグループが存在することを示します。この現象の一般的な兆候は、スイング マップの中心線から 1 シグマ以内に 15 回の連続スイングがあることです。これを見つけた場合は、サブグループ内で層別化の可能性があるかどうかを確認してください。サブグループ内の層別が平均マップにどのような影響を与えるかを理解するには、図 8 の平均管理図の管理限界 (主に LCL=4 ~ UCL=15) と図 10 の管理限界 (主に LCL=8 ~ UCL=11) を比較します。
サブグループ内の変動を最小限に抑えます。 背景雑音レベルは、サブグループ内の変動によって決まります。このノイズを背景にして信号を探す必要があります。サブグループ内の変動を最小限に抑えることで、プロセス挙動管理図の感度を最大化します。
サブグループ間の変動の機会を最大化します。 これには、データ ストリーム内でどのような種類の潜在的な信号が発生する可能性があるかを考える必要があります。 2 つのものを比較したい場合は、それらを異なるサブグループに配置する必要があります。 2 つのものが異なる可能性がある場合、それらは異なるサブグループに属する必要があります。
サブグループ内にシグナルを埋め込まないでください。 グループ化は、サブグループが均一に保たれる範囲でのみ有効です。パラメータ推定が目的である統計の多くの分野では、大量のデータが好まれます。ただし、これは平均サブグループと範囲サブグループの XbarR チャートには適用されません。サブグループのサイズを大きくすることは、サブグループの均一性を壊す良い方法です。計算ではサブグループの内部均一性が明示的に仮定されているため、サブグループの論理的均一性はサブグループのサイズよりもはるかに重要です。
データのコンテキストを尊重します。 コンテキストはデータの構造を定義し、プロセスを変更するときに変動の特定の原因を発見するための鍵となります。サブグループの順序さえも重要になる場合があります。通常、グラフに時間順を使用するのはこのためです。ただし、データのコンテキストで意味がある場合は、他の順序を使用することもできます。
秘密の質問
図 8 と 10 の暗黙の仮定のうち、間違っているものはどれですか?
当社のソフトウェア 「シューハート管理図 PRO-Analyst +AI(Windows、Mac、Linux用)」 には、この記事のデータを含む準備済みの Excel ファイルがすでに含まれています。